课程链接

§0 Preliminaries

证明方法：数学归纳法、反证法

language：string的set

language operations：

交、并、减

补： $\overline{L}$ = Σ* - L

reverse：L^R^ = {w^R^: w∈L}

concatenation：L~1~L~2~={xy: x∈L~1~, y∈L~2~}

L^4^=LLLL，L^0^ = {ε}

L^^=L^0^∪L^1^∪L^2^∪L^3^……，L^+^=L^^- {ε}

string：alphabet中的symbol构成的list

string operations:

concatenation拼接，记作w~1~w~2~

reverse转置，记作w^R^

string length，记作

w

substring，子串

幂：w^4^=wwww，w^0^=ε

alphabet (Σ)：symbol的finate set有穷集合

※ Σ*：某个字母表Σ可构成的所有string的集合，Σ^+^ = Σ* - ε

※ ε：空串，长度为0的字符串

注意：利用数学归纳法证明字符串相关问题，归纳假设从ε开始

§1 Finite Automata

有穷自动机FA

基本元素：state、inputs、transitions等

state：start、final等，final在图中一般表示为双圈

accepted（end）：所有input读完并停在final state上

※ 强调所有input读完是因为final state可能有出边

确定性有穷自动机DFA

定义

1. A finite set of states (Q, typically).

2. An input alphabet (Σ, typically).

3. A transition function (δ, typically).

4. A start state (q~0~, in Q, typically).

5. A set of final states (F ⊆ Q, typically).

Transition function 迁移函数

δ(q, a) = 当前状态q，接收的下一个输入a，接下来的状态

δ函数是一个total function，即必须要有下一步存在，如果没有（final state），为其添加dead state，不过一般不管

扩展：第二个参数扩展为string

※ 一般地，abc……表示字母，wxyz……表示字符串

Basis: δ(q, ε) = q

Induction: δ(q, wa) = δ(δ(q, w), a)

表示方法

Graph

Q用nodes，迁移函数用arcs（箭头）

迁移表

为其建表，详见PPT 34

正则语言

※ 语言 for automaton A，L(A) = set of strings w, such that δ(q~0~, w) in F

正则语言：DFA可接受的语言

即：可以构造一个DFA，其经历L(A)后到达final end

反过来，非正则语言即不能被DFA接受的语言

e.g. 一个非正则语言：L~1~ = {0^n^1^n^

n≥1}

证明其非正则：

假设可被某有m个状态的DFA接受，对于字符串0^m^1^m^

在前m步中（即连续处理m次0输入），变化了m+1个状态，由鸽笼原理PHP，必然有重复状态，即：前m步中存在环，设S~i~ = S~j~ = q

那么，对于字符串0^m-j+i^1^m^，这个DFA也能接收（去掉环）

所以，不存在这样的DFA

非确定性有穷自动机NFA

定义

1. A finite set of states, typically Q.
2. An input alphabet, typically Σ.
3. A transition function, typically δ.
4. A start state in Q, typically q~0~.
5. A set of final states F ⊆ Q.

不同：δ(q, a) is a set of states

Basis: δ(q, ε) = {q}

Induction: δ(q, wa) = the union over all states p in δ(q, w) of δ(p, a)，

即∪(δ(p, a), p∈δ(q, w))

DFA与NFA等价

左到右显然

右到左：子集构造法

states：2^Q^（幂集，即所有子集构成的集合）

start state：{q~0~}

final state: 元素中有F的成员的

即，将{……}视为一个状态，证明见PPT 85&86

NFA With ε-Transitions

存在ε-Transitions，即不用任何输入就可以转移

状态闭包：CL(q) = 从q，仅通过ε可走到的集合（可以多次ε）（包括自身）

Basis: δ(q, ε) = CL(q)

Induction: δ(q, wa) = $\cup{CL(\delta(p,\ a))\

\ p \in S=\delta(q,\ w)}$

语言：δ(q~0~, w) 含有final state

NFA与NFA With ε-Transitions等价

详细证明见PPT 92

左到右显然（看作不含ε的NFA with ε），右到左：①把经ε可到的加入到新的NFA的结果；②对于finalstate，凡是经过ε可到final state的都算新的final state

Summary

• DFA，NFA，NFA with ε等价，都接受正则语言

• 在建模上，NFA等可能更好地表达，可能状态更少
• 仅有DFA可被实现

§2 Regular Expressions

正则表达式RE

介绍

正则表达式能够表达正则语言

操作符

Union 语言的并

Concatenation 语言的连接

Kleene star 语言的*

详见第0章

R + ∅ = R

εR = Rε = R

∅R = R∅ = ∅

定义

Basis 1 如果a是symbol，那么a是RE，L(a) = {a}

Basis 2 ε是RE，L(ε) = {ε}

Basis 3 Ø是RE，L(Ø) = Ø

Induction 1 如果E~1~和E~2~是RE，那么E~1~+E~2~是RE，L(E~1~+E~2~) = L(E~1~)∪L(E~2~)

Induction 2 E~1~E~2~是，L(E~1~E~2~) = L(E~1~)L(E~2~)

Induction 3 如果E是RE，那么E*是，L(E*) = (L(E))*

※ 优先级：* > 连接 > +

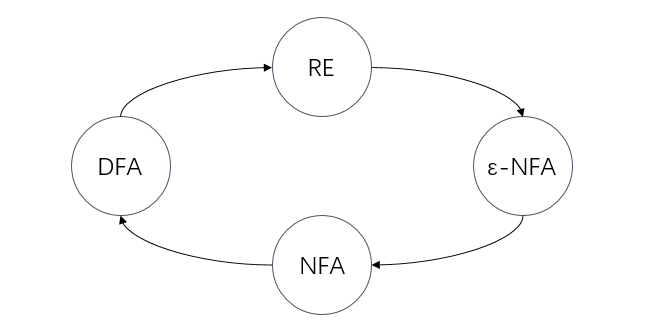
DFA→RE：见PPT 20起，用k-Path（类似Floyd-Warshall）

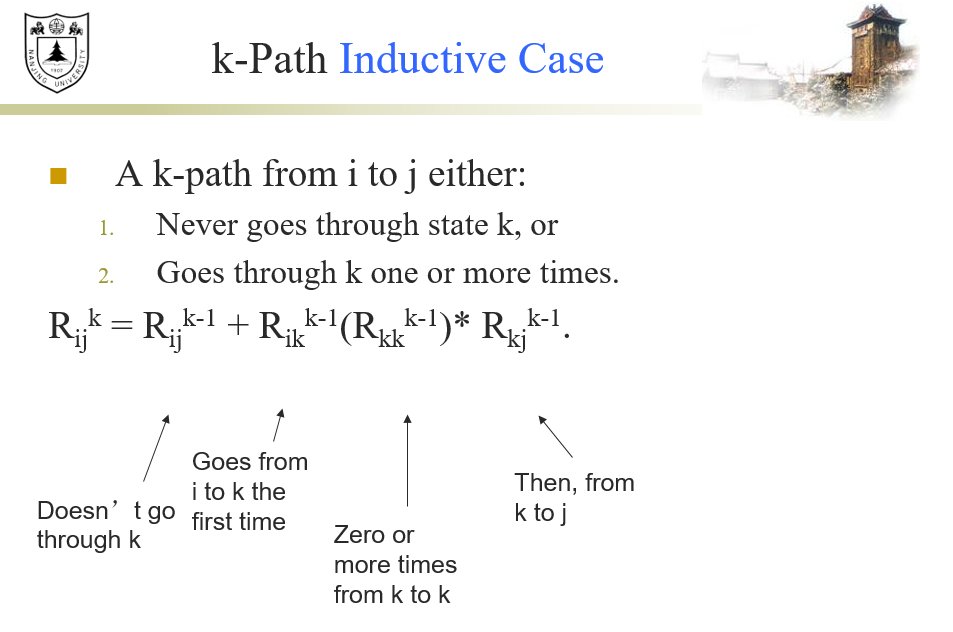
RE→ε-NFA：见PPT 10起（构造自动机）

正则语言的性质

language class

具有同一性质的多种语言的集合，如正则语言的集合

封闭性：若语言类中任挑2个作某运算得到的语言仍然属于该类，称该语言在该操作下封闭

判定性

聚类、一个语言的最小的表达、两个语言的等价判断

Membership problem string w是否在L中：在自动机中走一遍

Emptiness problem 是否是空语言：判断DFA中终点是否可达

Infiniteness problem 是否无穷：①成环即无穷，故找环

②If an n-state DFA accepts a string w of length n or more, then there must be a state that appears twice→无穷

second key idea（保证算法的终止）：如果有L可接收的大于n的string，则必然有长度在n到2n-1间的也可被L接受

→Test for membership all strings of length between n and 2n-1

The Pumping Lemma (for regular language)

For every regular language L

​ There is an integer n, such that

​ For every string w in L of length > n

​ We can write w = xyz such that:

1. xy

   < n.

2. y

   > 0.

3. For all i > 0, xy^i^z is in L.

例子见PPT 56，用于证明一个语言不是正则语言

※ n不是随便取的！

等价性

DFA间是否一致

证法：乘积自动机：作笛卡尔积得到新的状态（实际上相当于两个自动机各走各的的全局状态） 见PPT 59起

终止状态：其中一个终止，另一个不终止 PPT 61

$L = M \iff$ 该乘积自动机为空（不可能出现一个终止另一个不终止）

L是M的子集

同样做乘积自动机

终止状态：L终止，M不终止

$L \subset M\iff$ 自动机为空

Minimum-State

需要先判断等价性

构建状态表，判断两个状态能否区分（接受某字符串，仅一个到终止）

Basis：Mark每一个[final state和非final state]对

Induction：Mark pair[q, r] if for some input symbol a, [δ(q, a), δ(r, a)] is marked

如果不再有可mark的（闭包），未被mark的equivalent且可被merge into one state

→压缩：设q1到qk是不可区分的状态，则可被压缩成一个状态q；然后，δ(q1, a)…δ(qk, a)是不可区分状态（否则至少有一个会被mark）

这样得到的是最小的DFA，证明见PPT 79起

封闭性

若语言类中任挑2个作某运算得到的语言仍然属于该类，称该语言在该操作下封闭

①并、连接、*

（用正则表达式直接证明）

②交（乘积自动机，final state为二者都final，则该乘积自动机为二者的交，则是正则语言），类似的，差也是（final state为仅前者final），因此补也是（Σ*-L）

③逆（用正则表达式证明 PPT 94起）

④同态映射：把字母表中的每个元素映射到一个字符串，e.g.h(0) = ab

若L是，则h(L) = {h(w)

w in L}也是

证明直接用正则表达式 PPT 99

⑤逆同态：e.g. h(0) = ab, h(1) = ε，L = {abab, baba}，则h^-1^(L) = L(1*01*01*)

即，h^-1^(L) = {w

h(w) is in L}

构造方法见PPT 104

在上述例子中，设DFA A读取ab串，B读取01串，则B读0→A读h(0)即走ab从而得到迁移函数

※PPT中的例子不是上述例子

§3 Context-Free Grammars

CFG Formalism

Terminals 终止符

Variables = nonterminals （和Terminals集合不相交）

Start symbol 初始变量

production 产生式 variable->string of variables and terminals

一般地，

ABC，S大写字符表示variable

abc表示alphabet内的具体字符（terminals）

XYZ表示是terminal或variable

wxyz表示terminal构成的string

αβγ表示一切string

e.g. CFG for { 0^n^1^n^

n ≥ 1}

Terminals = {0, 1}.

Variables = {S}.

Start symbol = S.

Productions =

​ S -> 01

​ S -> 0S1

※ 若将第一个改为S->ε，则n≥1改为n≥0

Derivation

We say aAb => agb if A -> g is a production

n=>* means “zero or more derivation steps.” (0到多步可推导)

上下文无关语言 CFL

if G is a CFG, then L(G) = {w

S=>* w}

可用CFG define的语言就是CFL

※ CFL只能count two things, not three

BNL Notation

1. Variable <xxx>
2. Terminal 加粗或下划线
3. 产生式 ::=

4. or

5. 出现一或多次 ··· *※α··· 即 A-> Aα

   α*

6. 可选 [xxx]

lm，rm

lm（left most）：展开左边第一个Variable，rm则右边第一个

语法分析树 Parse Tree

叶子节点：terminal或ε

中间节点：variable

根节点：start symbol

father与child关系：production

yield：从左往右读所有叶节点

语法树$\iff$推导

证明见PPT 37起

文法的歧义

CFG有歧义$\iff$有一个string in CFG，可由两棵及以上语法树生成，即有两个不同的左/右推导

※ grammar有歧义，language不一定有（同一个language可以有多个grammar写出）

LL(1) Grammar

每次从左向右只看第一个字符，且仅有一种选择，故可以保证没有歧义

一般一个编程语言都有一个LL(1)

有些语言必有歧义，比如{0^i^1^j^2^k^

i=j或j=k}，当i=j=k时（PPT 62）

CFG范式 Normal Forms

Eliminating Useless Variables

useless有两种：

1. 推导不出terminal string的，例如B->bB（Variables That Derive Nothing）

   对于这种，删去其以及含其的production，例子见PPT 73

2. 从s走不到的（Unreachable Symbols）

   顺序：先删1再删2（删1会诞生新的2）

Removing Epsilon ε

if L is a CFL, L-{ε} has a CFG with no ε-productions

Nullable Symbols = A such that A =>* ε

Basis: If there is a production A -> ε, then A is nullable.

Induction: If there is a production A -> α and all symbols of α are nullable, then A is nullable.

※ Nullable是可空而不是一定空，故若A -> B

C，S -> AB, S’->AC, B-> ε，则B、A、S可空

删除思想 S->α，α中任何Nullable都可存在可不存在（枚举）

*e.g. S -> ABC, A -> aA

ε, B -> bB

ε, C -> ε*

A, B, C, and S are all nullable.

S -> ABC

AB

AC

BC

A

B

C ※虽然ABC都可空，但不需要添加S->ε

A -> aA

a（由aA，A=>ε产生）

B -> bB

b

※ C变成了useless

Note

1. 删ε会产生useless
2. 删ε会产生单元产生式

Removing Unit Productions

单元产生式Unit Productions body只有一个variable

Key idea: If A =>* B by a series of unit productions, and B -> a is a non-unit-production, then add production A -> a.

Then, drop all unit productions

Theorem: if L is a CFL, then there is a CFG for L – {ε} that has:

1. No useless symbols.

2. No ε-productions.

3. No unit productions.

I.e., every body is either a single terminal or has length > 2.

由前面，我们有如下clean顺序：

1. ε-productions（删除会产生unit等）
2. unit productions（删除会产生useless）
3. useless（删除会产生unreachable）
4. unreachable

Chomsky Normal Form

乔姆斯基范式CNF：every production is of one of these two forms:

1. A->BC
2. A->a

故，可用二叉树表示

Theorem if L is a CFL, then L-{ε} has a CFG in CNF

HOW?

Step 1: “Clean”，从而得到body is either a single terminal or of length at least 2

Step 2: For those length ≥ 2, replace, e.g. A->Bcd => A->BA~c~A~d~, A~c~->c, A~d~->d

现在，要么是到terminal，要么是到≥2的variables

Step 3: replace, e.g. A->BCDE => A->BF, F->CG, G->DE

§4 Pushdown Automata

PDA 下推自动机

Definition

PDA和CFG在语言定义上等价

非确定PDA可define all the CFL’s

确定性PDA可表示parsers（解释器）

ε-NFA with 栈，移动取决于当前状态、当前输入、当前栈顶

In each choice, the PDA can:

1. Change state, and also
2. Replace the top symbol on tht stack by a sequence of zero or more symbols
   • Zero symbols = “pop”
   • Many symbols = sequence of “pushes”

A PDA is described by:

1. states Q
2. input alphabet Σ
3. stack alphabet Γ（GAMMA）
4. transition function δ（delta）
5. start state q~0~ in Q
6. start symbol Z~0~ in Γ
7. final states F ⊆ Q

输入参数：q in Q，input a， stack symbol Z

δ(q, a, Z) is a set of zero or more actions of the form(p, α)，p是state，α是一串stack symbols

e.g. 0~n~1~n~ PPT 10起

计数！

ID instantaneous description计时描述

三元组(q, w, α)， q是当前状态，w是剩余输入，α是当前栈串，top在left

Goes-To: To say that ID I can become ID J in one move of the PDA, we write I⊦J

Formally, (q, aw, Xa)⊦(p, w, ba) for any w and a, if δ(q, a, X) contains (p, b).

Extend ⊦ to ⊦*, meaning “zero or more moves,” by:

• Basis: I⊦*I.

• Induction: If I⊦*J and J⊦K, then I⊦*K.

例子见PPT 24

Theorem 1: Given a PDA P, if (q, x, a)⊦* (p, y, b) , for all the string w in Σ* and all the string γ in Γ*, we have (q, xw, aγ)⊦* (p, yw, bγ) （在从q转换到p的过程中没有碰到w和γ） ，反过来不成立

Theorem 2: Given a PDA P, if (q, xw, a)⊦* (p, yw, b) , we have (q, x, a)⊦* (p, y, b)

Languages of the PDA

final state定义：

If P is a PDA, then L(P) is the set of strings w such that (q~0~, w, Z~0~) ⊦* (f, ε, a) for final state f and any a

empty stack定义：

If P is a PDA, then N(P) is the set of strings w such that (q~0~, w, Z~0~) ⊦*(q, ε, ε) for any state q

Equivalence 表达能力的等价性

1. If L = L(P), then there is another PDA P’ such that L = N(P’).

2. If L = N(P), then there is another PDA P’’ such that L = L(P’’).

   证明见PPT 30（构造性证明注意，我能做你能做的，且没有引入新的，即不能做你不能做的）

Deterministic PDA’s DPDA

一次至多一个选择

可以有ε，但是δ(q, a, X)和δ(q, ε, X)不能同时非空

PDA vs DPDA

RE < DPDA(L(P)) < NPDA

RE 无法推出< DPDA(N(P)) 不存在强弱关系

DPDA(N(P)) < DPDA(L(P))

※DPDA的N(P)与L(P)不相同

DPDA and Ambiguity

给定DPDA P，L = L(P)，L有无歧义文法；但并非无歧义文法都有DPDA表示

e.g. ww^r^ S->0S0

1S1

ε

Equivalence of PDA, CFG

CFG to a PDA

• Let L = L(G).

• Construct PDA P such that N(P) = L.

• P has:

  • One state q.
  • Input symbols = terminals of G.
  • Stack symbols = all symbols of G.
  • Start symbol = start symbol of G.

假设每一步P都表达某次左推导

假设当前P的栈是α，P目前消耗了字符串x，那么P目前表达了左推导S =>* xα

空栈时相当于接收了一个L(G)内的字符串

Transition Function of P

1. δ(q, a, a) = (q, ε). (Type 1 rule)

   处理终止符，逐步往前走

2. If A->α is a production of G, then δ(q, ε, A) contains (q, α). (Type 2 rule)

   A pop出去，α push进来

证明N(P) = L(G) 见PPT 51起

实际上是证明(q, wx, S) ⊦* (q, x, α) for any x $\iff$ S =>*~lm~ wa

再let x = a = ε

(q, w, S) ⊦* (q, ε, ε) $\iff$ S =>*lm w.

That is, w is in N(P) $\iff$ w is in L(G).

PDA to a CFG

• Let L = N(P)
• construct a CFG G such that L = L(G)

净效果[pXq] ：从p走了n步到q后恰好消耗了栈中的X（栈中X下面的东西没变）这样的一个字符串

将G的变量均写为这样的形式

This variable generates all and only the strings w such that

(p, w, X) ⊦*(q, ε, ε).

详细见PPT 57起

Example见PPT 68

We can prove that (q~0~, w, Z~0~) ⊦*(p, ε, ε) $\iff$ [q~0~Z~0~p] =>* w.

§5 CFL2

※ 与正则语言泵引理不同！

The Pumping Lemma for CFL’s

Statement

For every context-free language L

​ There is an integer n, such that

​ For every string z in L of length > n

There exists z = uvwxy such that:

1. $

   vwx

   \le n$.

2. $

   vx

   > 0$. //不同时为空

3. $For\ all\ i \ge 0, uv^iwx^iy\ is\ in\ L$.

Proof

将L-{ε}用CNF（乔姆斯基范式）表达

设有m个variables，$n=2^m$

若有长度≥n的z，则在语法生成树上yield z必有≥m+2的路，必经过至少m+1个variables，则we can find two nodes with the same label, say A

详见PPT 5 起

Applications

证明不是CFL

一般都需要分类讨论（vwx在中间，故可能有多种情况）

※ n不是随便取的！

Properties of Context-Free Languages

Decision Properties

Testing Emptiness

看Start Symbol是不是useless variables（3.5.1）

Testing Membership

看串在不在语言里

RL：在DFA中跑一遍（因为可以是DFA，是确定的）

表达成CNF（空串单独讨论，看Start Symbol是否Nullable）

CYK算法（一种dp算法）

见PPT 19起

Testing Infiniteness

与RL相同

Closure Properties

• CFL’s are closed under union, concatenation, and Kleene closure.

• Also, under reversal, homomorphisms（同态） and inverse homomorphisms.

• But not under intersection（交） or difference（差）.
• But under intersection with RL

§6 Turing Machine

Turing Machines

Turing Machine Theory

Formalism

A TM is described by:

1. A finite set of states (Q, typically).
2. An input alphabet (Σ, typically).
3. A tape alphabet (Γ, typically; contains Σ).
4. A transition function (δ, typically).
5. A start state (q0, in Q, typically).
6. A blank symbol (B, in Γ- Σ, typically).

• All tape except for the input is blank initially. 即指示该位置是否有内容，没有则为B
  1. A set of final states (F ⊆ Q, typically).

• a, b, … are input symbols.

• …, X, Y, Z are tape symbols.

• …, w, x, y, z are strings of input symbols.

• α, β,… are strings of tape symbols.

Transition Function:

Takes two arguments:

1. A state q, in Q.

2. A tape symbol Z in Γ.

δ(q, Z) is either undefined or a triple of the form (p, Y, D).

• p is a state.

• Y is the new tape symbol.

• D is a direction, L or R.

※ halt: 停下

Instantaneous Descriptions ID

αqβ：α是左边的非blank，β是右边的（包括当前指向的，因为当前指向的是待处理而还没有处理的）

1. If δ(q, Z) = (p, Y, R), then
   • $αqZβ ⊦ αYpβ$
   • $If\ Z\ is\ the\ blank\ B,\ then\ also\ αq ⊦ αYp$
2. If δ(q, Z) = (p, Y, L), then
   • $For\ any\ X,\ αXqZβ⊦αpXYβ$（把Z改为Y，然后向左走）
   • $In\ addition,\ qZβ⊦pBYβ$

Language of a TM

Final State:

L(M) = {w | $q_0w$ ⊦* I, where I is an ID with a final state}.（不是停在final state）

Halting:

H(M) = {w | $q_0w$ ⊦* I, and there is no move possible from ID I}.

不改变能力:（与PDA一样，不是说L与H等价，而是说表达能力相同）

1. If L = L(M), then there is a TM M’ such that L = H(M’).

2. If L = H(M), then there is a TM M” such that L = L(M”).

证明见PPT 22起

Recursively Enumerable Languages RE

递归可枚举语言，可用TM define的语言

//图灵可识别语言

Recursive Languages RL

递归语言 //图灵可判定语言

An algorithm is a TM, accepting by final state, that is guaranteed to halt whether or not it accepts

RE＞RL：L = L(M) for some TM M that M is an algorithm

※递归语言：输入W，给y/n（一定可以停下来）；

※递归可枚举：输入W，可能给y（可能一直运行下去直到给yes，不保证有no）

Every CFL is a recursive language

More about TM

“Programming Tricks”

多磁道和Cache都不会改变表达能力

Multiple Tracks

多磁道

图见ppt 38

可用于加flag（Marking）

Caching in the state

TM with Storagae

Multitape Turing Machines

不改变表达能力（k tapes可用2k tracks模拟）

Nondeterministic TM’s

The TM accepts its input if any sequence of choices leads to an accepting state

NTM与DTM等价：PPT 63起

Closure Properties of Recursive and RE Languages

结论：

• 均在union, concatenation, star, reversal（转置）, intersection（交）, inverse homomorphism（逆同态）下封闭；
• Recursive在difference（差）, complementation（补）下封闭
• RE在homomorphism下封闭

证明见PPT 79 起

§T1 TM’s Decidability

图灵机是countable，语言不是，故有图灵机不可识别的语言

Halting Problem

HALT = { <M, x>

TM M halts on input x }

summary见PPT 26

Complexity

further classify decidable problems

worst-case analysis:f(n)

f(n) is the maximum number of steps M uses on any input of length n

大O: f(n) = O(g(n)) if there exist positive integers $c, n_0$ such that for all $n ≥ n_0$

$f(n) ≤ cg(n)$

Time complexity class：TIME(t(n)) = {L

there exists a TM M that decides L in time O(t(n))}，即是复杂度为O(t(n))的语言的集合

Theorem: Let t(n) satisfy t(n)≥n. Every t(n) multitape TM has an equivalent O(t(n)2) single-tape TM

P

$P = \cup_{k ≥ 1} TIME(n^k)$

(on a deterministic single-tape Turing Machine)

NP

$NP = \cup_{k ≥ 1} NTIME(n^k)$

NTIME(t(n)) = {L

there exists a NTM M that decides L in time O(t(n))}

Theorem: language L is in NP if and only if it is expressible as:

$L = { x\

\ \exist y,

y

≤

x

^k, <x,y> \in R }$

R关系是P内的一个语言

即算法课提到的多项式时间可判定

※EXP：$EXP = \cup_{k ≥ 1} NTIME(2^{n^k})$

关系见PPT 62

NPC and NP-hard

NP-hard: every A in NP is is polynomial time reducible to B, then B is NP-hard.

NPC: NP-hard & NP

Reduce

reductions归约

Theorem: if $A ≤_m B\ $and B is decidable, then A is decidable

Main use: given language NEW, prove it is undecidable by showing $OLD ≤_m NEW$, where OLD is known to be undecidable

常用undecidable：

• $HALT$ = {<M, w> : M halts on input w}
• $A_{TM}$ = {<M, w> : M accepts input w}
• $E_{TM}$ = {<M> : L(M) = Ø}

Rice Theorem: Every nontrivial TM property is undecidable.

nontrival见PPT 82

Wikipedia：

Let S be a set of languages that is nontrivial, meaning

1. there exists a Turing machine that recognizes a language in S,
2. there exists a Turing machine that recognizes a language not in S.

Then it is undecidable to determine whether the language recognized by an arbitrary Turing machine lies in S.

SAT

SAT is NPC (The Cook-Levin Theorem)

Others

PSPACE,coNP,……

Church-Turing Thesis

everything we can compute on a physical computer can be computed on a Turing Machine in time t(n)O(1) (polynomial slowdown)kl

§7 Transition System

Defination

A transition systems is a tuple $A=<S,S_0,T,α,β> $ where

• $S$ is a finite or infinite set of states
• $S_0$ is initial location
• $T$ is a finite or infinite set of transitions
• $α$ and $β$ are two mapping from $T$ to $S$ which take each transition $t$ in $T$ to the two states $α(t)$ and $β(t)$, respectively the source and the target of the transition t.

迁移系统没有final

有穷迁移系统：S和T有穷

Paths

$t_1, t_(2,)⋯t_n,⋯$ such that:

$∀i:1≤i,β(t_i)=α(t_{i+1}),\ and\ α(t_1)=S_0$

s→s’、s↠s‘、s is reachable见PPT 7

terminal：终点

死锁deadlock：reachable and terminal

$T^+$:有穷路径的集合；$T^ω$:无穷路径的集合

$α(path)=α(t_1),\ β(path)=β(t_n)$，路径终点仅存在于有穷路径

点乘∙ $\beta(c)=\alpha(c’)$，则$\alpha(c∙c’)=\alpha(c),\ \beta(c∙c’)=\beta(c’)$

ε：见PPT 10

Labeled trasition systems

拓展λ：$A=<S,S_0,T,α,β,\lambda> $

λ is a mapping from T to A taking each transition t to its label λ(t)

path→trace；

Equivalency

同态homomorphism：见PPT 17起

强同构：

存在双射（一一对应）的同态函数，则等价

弱同构：

可达集上强同构，则等价

双仿真bisimulation：

定义见PPT 24，例图见PPT 25，

在产生分歧的地方一一对应，即在同样时刻做选择

Product

global system中

free product

$A=A_1× A_2 … ×A_n$

$S=S_1× S_2 …× S_n$

$T=T_1× T_2 …× T_n$

$α(t_1 “, “ ⋯,t_n )=⟨α_1 (t_1), ⋯,α_n (t_n )⟩$

$β(t_1 “, “ ⋯,t_n )=⟨β_1 (t_1), ⋯,β_n (t_n )⟩$

约束

transition的发生是同时的（同步）

1. 同步约束，某些transiton不能同时触发
2. τ transiton，允许product中某者原地踏步
3. share label，product中的共享label，某些事件必须同步发生

CTL*

定义见PPT 52

Path quantifiers and Temporal operators

Path quantifiers:

• A ( for all computation path )

• E ( for some computation path )

Temporal operators:

• X next time
• F eventually / future
• G always / globally
• U until
• R release

a U b：在某state上如果b在某处hold，在之前a一直为true、

a R b：b在a holds前（包括刚holds）一直正确

示例见 62

嵌套处理：AG.AF.p ⇨ AG.φ φ→AF.p

§8 Petri Nets

concurrent, asynchronous, distributed, parallel, nondeterministic and/or stochastic systems

Definition

Informal

The graphical presentation of a Petri net is a bipartite二分 graph

There are two kinds of nodes

• Places: usually model resources or partial state of the system

• Transitions: model state transition and synchronization

Arcs 有向边， connect nodes of different types

Tokens are resources in the places

definition

C = ( P, T, I, O)

• P：places集合
• T：transitions集合
• I/O：每个transiton的input、output，表示为·t、t·

marking μ为资源分布 PPT 13中μ=1010

state：token在图中的布局

fire：触发，enable transition can fire and result in a new marking

• Firing of a transition t in a marking is an atomic operation

enable：t的每个input有足够的token

run：见PPT 21

weight edges：消耗和产生token为权重

finite capacity ：places有capacity，到了后不能触发

Removing Capacity Constraints 见PPT 31起

各种Example见PPT 33起

Properties

Property

Sequential顺序、synchronization同步、merging、fork、concurrency并发、non-deterministic、conflict冲突

Behavioral property

Properties that depend on the initial marking

safety 坏的不发生

liveness 好的会发生

fairness 每种可能下都会发生

1. Reachability 可达性，
   • Mn is reachable from M0 if exists a sequence of firings that transform M0 into Mn
2. Boundedness
   • 指的是for any marking，reachable from M0的places的token不超过k则称为k-bound
   • 1-bound又叫safe
3. liveness 又叫deadlock-free
4. reversibility 可逆
5. persistence 不争夺，一个fire不影响另一个
6. fairness
   • bounded-fairness: the number of times one transition can fire while the other is not firing is bounded
   • unconditional(global)-fairness: every transition appears infinitely often in a firing sequence
7. coverability tree 见PPT 53

Reduction rules简化

见PPT 61起

Time Extension

在transition上加上时间窗口[a,b]，在窗口内允许fire，fire操作不花时间

计时开始是相对于enable时，假设c时刻enable，则允许的fire时间为[c + a; c + b]，最迟在c + b必须fire；

Time Petri: N =(P,T,F,Eft,Lft,μ0), where:

• P = {p1, p2,…,pm} is a finite set of places;
• T = { t1, t2,…,tn } is a finite set of transitions (P∩T=∅)
• F⊂(P×T)∪ (T×P) is the flow relation;
• Eft,Lft:T→N are functions for the earliest and latest firing times of transitions, satisfying that for any t∈T, Eft(t) ≤Lft(t) ≤∞;
• μ0 ∈ P is the initial marking of the net.

由于transiton不消耗时间，故存在Zeno-behavior：一连串的zero-time transitons，即形如[0,b]的区间且都在0处fire

§9 Timed Automata

What is TA?

• an automaton with locations (即states) and edges

• the automaton spends time only in locations, not in edges

• real valued clocks (x, y, z)

• all clocks run at the same speed

• clock constraints can be guards on edges //guard即满足约束条件才允许通过
• clocks can be reset when taken an edge， only a reset to value 0 is allowed
• location invariants forbid to stay in a state too long, which force taking an edge

Definition

A = (L, X, I0, E)

• L is a finate set of locations
• X is a finite set of clocks
• I0 ∈ L is an initial location (start)
• $E \subseteq L\times C(X)\times 2^X\times L$ is a set of edges

对于edge，即起点、约束条件、reset clocks、终点

Clock Valuations

function用于改变时钟，详细定义及example见PPT 19起

Semantics

timed automata的语义是个transition system，见PPT 22起

Reachability Problem

Theorem：

The reachability problem is PSPACE-complete. (which is decidable)

证明思想：划分等价类

Extension

parallel composition

fischer’s protocal (share variable)

Hybrid System

混成系统 （离散与连续混合）

§Summary

Automata

DFA：组成（多元组）、string怎么走怎么停

NFA：是什么（选择虽然不止一个但有穷）、接收什么string

ε-NFA：定义

三者转换：子集构造法……三者等价，定义regular language

正则表达式RE：定义、与FA转换

做写出DFA与RE这种题时不要用kpath、子集构造法等（来不及）

Pushdown Automata

PDA⋛CFL

L(P)、N(P) 表达能力等价

DPDA、NPDA

泵引理（与RE做区别）（必考一种）（不能假设y具体是啥）

Turing Machine

图灵可识别、RE递归可枚举

图灵可判定、递归语言、算法

在哪些里封闭

扩展的等价（多纸带等）

归约（必考）停机问题、ATM、ETM

对角法

看rice定理的证明

Decidability：P、NP、NP-hard、NPC、EXP

Decidability and closure property

RL：组合乘积

CFL：clean、CYK

TM：TM construction（必考，不要在完整字符串中间加B）

closure：给定一个语言，做blahblah后是什么 VS 给定几个不同language，做blahblah后是什么

operations between languages in different classes

Models

会用就行，不要会证明

Transiton System（定义、equivalence、temporal logic即CTL）

Petri Net（concurrency、token game、relation between PN&TS）（很有可能会让画）（第三个例子：给两个PN，让画TS，问在TS里俩PN是否等价）

Timed Automata（definition、特点：细粒度 连续时间域 model a real system）

examples看看PPT，自己画、以及拍的照

列车多段速度都不同→混成自动机，速度：dx/dt

※