算法设计与分析复习笔记,按教学顺序。
准备知识
RAM模型
三类操作:简单操作(比较两个元素、在图遍历时对一个节点染色等);复杂操作(循环和子程序调用);存储访问(对存储单元的w/r)
计算模型:易用性和精确性
算法设计及证明
算法问题的规约
输入:明确规定了算法接受的所有合法输入;
输出:明确规定了对于每一个合法的输入值,相应的输出值应该是什么
例如:
输入:任意两个非负整数a、b
输出:a、b的最大公约数
算法的证明——数学归纳法
弱归纳&强归纳
算法分析
性能指标:关键操作 critical operation
| 算法问题 | 关键操作 |
|---|---|
| 排序、查找、选择 | 元素的比较 |
| 图遍历 | 节点信息的简单处理 |
| 串匹配 | 字符的比较 |
| 矩阵运算 | 两个矩阵元素的简单运算 |
其余的辅助操作通常和关键操作呈线性关系
$D(n):算法输入集合,f(I):对于输入I的时间复杂度,Pr(I):输入I出现的概率$
最坏情况时间复杂度:
$W(n)=\max_{I\in D(n)}f(I)$
平均情况时间复杂度:
$A(n)=\sum_{I\in D(n)}Pr(I)*f(I)$
数学基础
渐进增长率
O:上界
定义
- $O(g(n))={f(n):{\exist}c>0,n_{0}>0,{\forall}n{\ge}n_{0},0{\le}f(n){\le}cg(n)}$
- $f(n)=O(g(n))\iff\lim_{n \to \infty}{\frac{f(n)}{g(n)}=c<\infin}$
含义
当n足够大时,f(n)的增长率不会超过g(n)的
或者说,如果一个任务是O(g(n)),其肯定能在c*g(n)时间完成(g(n)足够大,下同)
举例
n是O(n),logn也是
o:严格的等级差
定义
- $o(g(n))={f(n):{\exist}c>0,n_{0}>0,{\forall}n{\ge}n_{0},0{\le}f(n)<cg(n)}$
- $f(n)=O(g(n))\iff\lim_{n \to \infty}{\frac{f(n)}{g(n)}=0}$
含义
当n足够大时,f(n)的增长率小于g(n)的,即,总可以通过增加问题的规模使得f(n)和g(n)之间有任意大的差距
或者说,如果一个任务是o(g(n)),其肯定能在少于c*g(n)的时间完成
举例
logn是o(n)
Ω:下界
定义
- $\Omega(g(n))={f(n):{\exist}c>0,n_{0}>0,{\forall}n{\ge}n_{0},f(n){\ge}cg(n)}$
- $f(n)=\Omega(g(n))\iff\lim_{n \to \infty}{\frac{f(n)}{g(n)}=c>0}$
含义
当n足够大时,f(n)的增长率不会低于g(n)的
或者说,如果一个任务是Ω(g(n)),其至少要用c*g(n)的时间完成
举例
n是O(n),nlogn也是
ω:严格的等级差
定义
- $\omega(g(n))={f(n):{\exist}c>0,n_{0}>0,{\forall}n{\ge}n_{0},f(n)>cg(n)}$
- $f(n)=\omega(g(n))\iff\lim_{n \to \infty}{\frac{f(n)}{g(n)}=\infin}$
含义
当n足够大时,f(n)的增长率大于g(n)的,即,总可以通过增加问题的规模使得f(n)和g(n)之间有任意大的差距
或者说,如果一个任务是ω(g(n)),其无法在c*g(n)的时间完成
举例
n是ω(logn)
Θ:精确描述
定义
- $\Theta(g(n))={f(n):{\exist}c_1>0,c_2>0,n_0>0,{\forall}n{\ge}n_0,c_1g(n){\le}f(n){\le}c_2g(n)}$
- $f(n)=\Theta(g(n))\iff\lim_{n \to \infty}{\frac{f(n)}{g(n)}=c,c\in(0,\infin)}$
含义
f(n)与g(n)处于同一水平
或者说,如果一个任务是Θ(g(n)),其在c*g(n)的时间完成
举例
2n是Θ(n)
关于
- o、ω是传递的
- O、Ω是传递、自反的,即n=O(n)
- Θ是等价的,且f=Θ(g) iff f=O(g), f=Ω(g)
- 若f=O(g),则g=Ω(f),对于小的也一样

o:1,ω:2,O:1+3,Ω:2+3,Θ:3
数学运算背后的算法操作
取整、对数(略)
阶乘
Stirling公式:$n!=\sqrt{2{\pi}n}(\frac{n}{e})^n(1+\Theta(\frac1n))\approx\sqrt{2{\pi}n}(\frac{n}{e})^n$
常见级数求和
多项式级数:$\sum_{i=1}^{n}i=\frac{n(n+1)}2,\sum_{i=1}^{n}i^2=\frac13n(n+\frac12)(n+1),\sum_{i=1}^{n}i^k=\Theta(\frac1{k+1}n^{k+1})$
几何级数:$\sum_{i=1}^{k}r^i=\frac{r^{k+1}-1}{r-1}$
期望E[x]
指标随机变量:
$X_i=I{事件e_i}=\left{\begin{matrix}1,事件发生\0,事件未发生\end{matrix}\right.$
指标随机变量的期望值就等同于事件发生的概率
期望值的线性特征:
$给定X_1,X_2,…,X_k及其线性函数h(X_1,X_2,…,X_k),则有:$
$E[h(X_1,X_2,…,X_k)]=h(E[X_1],E[X_2],…,E[X_k])$
例如:$E[\sum x_i]=\sum E[x_i]$
求解递归方程
替换法
*若函数平滑(即f(2n)=Θ(f(n))),则对于$\left \lceil \right \rceil,\left \lfloor \right \rfloor $操作可以忽略
Guess and Prove \(e.g.T(n)=2T(n/2)+n \\ Guess:T(n)=O(nlogn)\\ Then\ need\ to\ prove:T(n)\le{cnlogn}\\ 根据归纳假设,我们有:T(n/2){\le}cn/2*log(n/2),所以\\ T(n)=2T(n/2)+n{\le}cnlog(n/2)+n{\le}cnlogn(取c{\ge}2)\) 需要注意的是,在上述证明中,套用定义只需在某个n~0~后成立即可,上述例子对于T(1)就不成立
递归树
分治递归的形式:$T(n)=aT(n/b)+f(n)$
a:划分为a个子问题;b子问题规模为原先的1/b;f(n):子问题划分与合并的代价
举例:
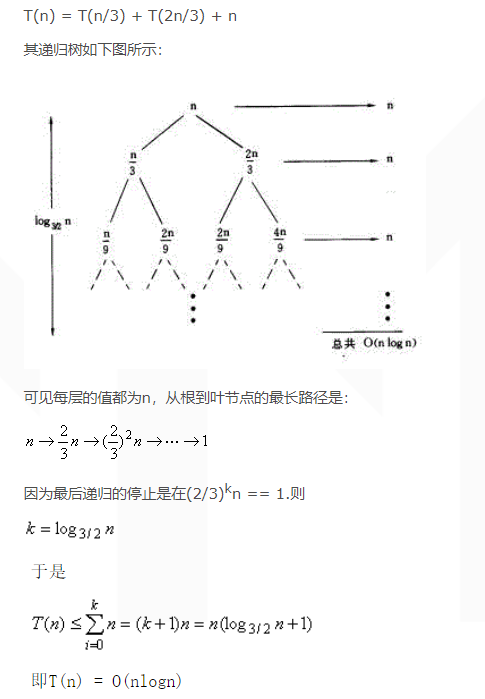
Master定理
对于:$T(n)=aT(n/b)+f(n)$,设$E=log_ba$ \(case\ 1:f(n)=O(n^{E-\epsilon}),\epsilon>0,then\\ T(n)=\Theta(n^E),公比大于1,等于叶子层\\ case\ 2:f(n)=\Theta(E),then\\ T(n)=\Theta(f(n)logn),公比等于1,等于层高*每层代价\\ case\ 3:f(n)=\Omega(n^{E+\epsilon}),\epsilon>0,and\ \exist c<1,af(n/b)\le cf(n),then\\ T(n)=\Theta(f(n)),公比小于1,等于根\) Master定理并没有涵盖所有情况,例如$T(n)=\sqrt nT(\sqrt n)+n$,可以用替换法进行求解
排序
线性表,从蛮力到快排
朴素排序
选择排序、冒泡排序
O(n^2^)
插入排序
每次取未处理的元素,在已处理的元素中排序
O(n^2^)
分治排序
快速排序
难分易和
def QuickSort(left,right):
if left<right:
middle=Partition(left,right)
QuickSort(left,middle-1)
QuickSort(middle,right)
def Partition(left,right):
pivot=A[left]#取基准元素
pivot_pos=left#基准元素的指针
for i in range(left+1,right+1):#from left+1 to right
if A[i]<pivot:
A[i],A[pivot_pos]=A[pivot_pos],A[i]#小的换到左边
pivot_pos+=1#发现一个小的,指针右移
A[left],A[pivot_pos]=A[pivot_pos],A[left]#完成交换,将基准元素放在正确的位置
return pivot_pos
在一次Partition中,数组A在[left,right]范围内,比pivot小的都移到了左边,故结束后pivot已处于数组中的正确位置,即左边都比其小、右边都比其大
分析:
最坏情况下(严格升序/降序),每次比较n且仅规模减小1,故为O(n^2^)
平均情况下
递归方程分析 \(划分情况等可能出现,即\\ A(n)=O(n)(Partition的代价)+{\frac1n}\sum_{i=0}^{n-1}[A(i)+A(n-1-i)]\\ =O(n)+{\frac2n}\sum_{i=0}^{n-1}A(n)\\ 用错项相减,可以算出A(n)=O(nlogn)\) 指标随机变量分析
根据之前的知识,设元素从a~0~到a~n~,定义指标随机变量$X_{ij}=I{a_i和a_j发生了比较}$
则快速排序的代价为$X=\sum_{i=1}^{n-1}\sum_{j=i+1}^{n}X_{ij}$
而平均情况时间复杂度为上述代价的期望值,即:
$E[x]=E[\sum_{i=1}^{n-1}\sum_{j=i+1}^{n}X_{ij}]=\sum_{i=1}^{n-1}\sum_{j=i+1}^{n}E[X_{ij}]=\sum_{i=1}^{n-1}\sum_{j=i+1}^{n}Pr{a_i和a_j发生了比较}$
将元素分为$a_0…a_{i-1},\ a_i,\ a_{i+1}…a_{j-1},\ a_j,\ a_{j+1}…a_n$五个部分,考虑当前基准元素处于哪个部分
部分①⑤:a~i~和a~j~是否发生比较取决于后续选择,即本次中未比较,可以不做考虑
部分③,a~i~和a~j~将分开到两个数组,永远不会比较
部分②④,选择其中一个作为基准元素,则其发生且仅发生一次比较
故发生比较的概率为 $\frac2{j-i+1}$
带入之前的式子,可以计算出时间复杂度为O(nlogn)
合并排序
易分难和
分而治之:先分为两部分,其在递归过程中已经排序完成,再将已经排好序的两部分合并
def MergeSort(left,right):
if left<right:
middle=(left+right)/2
MergeSort(left,middle)
MergeSort(middle+1,right)
Merge(left,middle,right)
def Merge(left,middle,right):
L=A[left:middle]
R=A[middle+1:right+1]
i=0,j=0
for k in range(left,right+1):#重新排列数组A[left:right+1]
if L[i]<R[j]: #更小的放在k上
A[k]=L[i]
i+=1
else:
A[k]=R[j]
j+=1
合并排序是典型的分治算法,其最坏情况时间复杂度为:
$W(n)=2W(n/2)+O(n)$
由Master定理,为O(nlogn),因此平均情况也为O(nlogn)(下界)
堆
定义
- 结构特性:完全二叉树
- 偏序特性:父大于子(or小于)
维护
修复
当堆顶元素被取走时修复
- 结构修复:将最后一个元素放到堆顶
- 偏序修复:自顶向下,若父最大或到底终止,否则与最大的那个交换,继续向下
由于层高为O(logn),每次修复操作为O(1),故复杂度为O(logn)
插入
与修复类似
- 结构:放在最后
- 偏序:自底向上,若父最大或到根终止
- 同样为O(logn)
构建
方法1:执行n次插入,O(nlogn)
方法2:递归,将每个子树整理成堆,然后执行一次修复(不删除元素)
最坏情况时间复杂度 $W(n)=2W(n/2)+O(logn)$,由Master定理,为O(n)
应用
假设具有如下堆函数:
def ConstructHeap(A,size)#将数组A整理成堆
def FixHeap_TopDown(A,pos,size)#从pos开始自顶向下执行堆修复
def FixHeap_DownTop(A,pos,size)#从pos开始自底向上执行堆修复
堆排序
def HeapSort(A,n):
size=n
ConstructHeap(A,size)
for i in range(n-1,1,-1):#从n-1到1
A[0],A[i]=A[i],A[0]#当前最大的元素被放在了当前的最后
size-=1
FixHeap_TopDown(A,0,size)
易得最坏情况下时间复杂度为O(nlogn)
优先队列
优先队列有如下接口:
GET_MAX(A) 返回优先级最高的元素
if len(A) is 0:
return error
return A[0]
EXTRACT_MAX(A) 返回优先级最高的元素,将其从队列中剔除
if len(A) is 0:
return error
max=A[0]
A[0]=A[len(A)-1]
del A[len(A)-1]
FixHeap_TopDown(A,0,len(A))
return max
INSERT(A, key) 添加新元素
A+=key
FixHeap_DownTop(A,len(A)-1,len(A))
INCREASE_KEY(A, i, key) 改变指定元素优先级
A[i]=key
FixHeap_DownTop(A,i,len(A))
基于比较的排序的下界
决策树
2-tree(子节点0或2),子节点0个的称为外部节点,2个的称为内部节点
在决策树中,内部节点表示的是(在父节点的比较之后)继续进行的新一轮比较,外部节点表示某一种排序结果,因此,h为走到某一次结果的代价,即某一次的时间复杂度
引理1 假设二叉树树高h,叶节点个数L,则L≤2^h^
定义:EPL 外部路径长度:根节点到所有叶节点路径长度之和
$EPL(T)=0,只有根节点;EPL(T)=EPL(T_L)+EPL(T_R)+N_L+N_R,其中N_L和N_R为左右子树的叶节点个数$
引理2 越平衡的2-tree,EPL越少
最坏情况时间复杂度的下界:对于n个节点,排序的结果一共有n!种,故决策树的叶节点至少有n!个,由引理1:
$n!\le L\le 2^h$
$h\ge log(n!)=\Omega(nlogn)$,即为下界
平均情况时间复杂度的下界:平均情况下的时间复杂度应该为$\frac{EPL}{L}$,由引理2,保证2-tree尽量平衡,则树高为$\Theta(L)$,EPL为$\Theta(LlogL)$,故对于任一相同节点的2-tree其EPL为$\Omega(L)$,则: $A(n)=\frac{EPL}{L}=\Omega(\frac{LlogL}{L})=\Omega(logL)=\Omega(log(n!))=\Omega(nlogn)$
选择
期望线性时间选择
在快速排序中,我们使用了Partition算法,该算法将基准元素移到了恰当的位置,代价为O(n),利用这个算法,我们可以得到:
def SelectElinear(left, right, k):#k:选择阶为k的数
if left == right:
return A[left]
m=Partition(left,right)#基准元素下标
x=m-left+1#在当前范围内,左边部分元素个数(包括自己)
if k==x:
return A[m]
elif k>x:#左边部分小于x个,在右边
return SelectElinear(m+1,right,k-x)
else:#左边部分大于x个,在左边
return SelectElinear(left,m-1,k)
虽然在最坏情况下为O(n^2^),但是在平均情况下,计算$A(n)=E[T(n)]的一个上界$
定义指标随机变量$X_k=I{小于等于基准元素的元素个数为k}$,由于概率相等,易得$E[X_k]=\frac1n$
$T(n)\le \sum_{k=1}^{n}X_k(T(max(k-1,n-k))+O(n))\\ \ \ \ \ \ \ \ =\sum_{k=1}^{n}X_kT(max(k-1,n-k))+O(n)$
每个子项的含义是在有k个小于或等于基准元素的个数的情况下所需的代价的上界
对其取期望,则有 \(E[T(n)]\le E[\sum_{k=1}^{n}X_k*T(max(k-1,n-k))+O(n)]\\ =\sum_{k=1}^{n}E[X_k*T(max(k-1,n-k))]+O(n)\\ =\sum_{k=1}^{n}E[X_k]E[T(max(k-1,n-k))]+O(n)\\ =\frac1n\sum_{k=1}^{n}E[T(max(k-1,n-k))]+O(n)\) 根据max函数的对称性,可以将其简化为
$E[T(n)]\le \frac2n\sum_{k=\frac n2}^{n-1}E[T(k)]+O(n)$
之后,用替换法可以证明其为O(n) \(假设O(n)=an,下面证明E[T(n)]\le cn\\ E[T(n)]\le\frac2n\sum_{k=\frac n2}^{n-1}ck+O(n)\\ =\frac{2c}n(\sum_{1}^{n-1}k-\sum_{1}^{\frac n2-1}k)+an\\ =\frac{c}n((n-1)n-(\frac n2-1)\frac n2)+an\\ \le cn-(\frac{cn}4-\frac c2-an)\) 只需要$\frac{cn}4-\frac c2-an\ge0$即可,即$n\ge \frac{2c}{c-4a}$
最坏情况线性时间选择
降低最坏情况下时间复杂度需要的是控制划分的平衡性
方法:
- 每五个数分为一组,进行一次划分,使得中位数位于中间
- 用所有小组中位数的中位数m*进行划分
- 之后的步骤与原算法类似
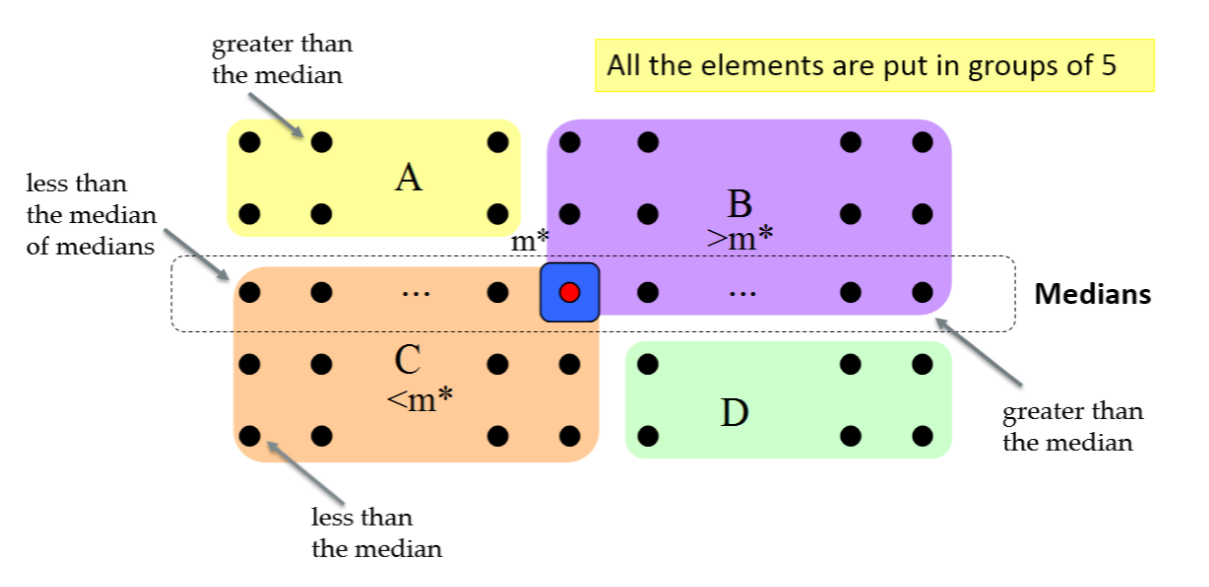
如上图,所有元素被m*划分为A、B、C、D四部分,其中B必然比m*大,C必然比其小,因此在一定程度上保证其平衡性。在最坏情况下,A、D元素也均比m*小,每次都要递归地到A、C、D三者中找,故其复杂度为:
$W(n)\le W(\frac n5)+W((\frac n{10})5+(\frac n{10}-1)2+3)+O(n)=W(\frac n5)+W(\frac7{10}n+6)+O(n)$
可以证明其为O(n)
查找
折半查找
查找算法
二分法
def BinarySearch(A, left, right, key):
if right<left:
return -1
mid=(left+right)/2
if key == A[mid]:
return mid
elif key < A[mid]:
return BinarySearch(A, left, mid-1, key)
else:
return BinarySearch(A, mid+1, right, key)
每次都缩小一半,故最坏情况O(logn)
要求:数组有序
折半查找的推广
查找峰值
有些数据具有单峰特性,可以利用折半查找
计算$\sqrt n$
折半查找,将中间值的平方和n对比
平衡二叉搜索树
二叉搜索树
对于树中任意节点,左子树均比它小,右子树均比它大
红黑树
定义
一些概念
- 颜色:红/黑
- 2-tree结构
- 外部节点:除非根是外部节点,否则外部节点不含有数据
- 黑色深度:根的黑色深度为0,其他节点的黑色深度为根到该节点的路径上黑色节点的个数(不包括根)
直接定义
- 根节点为黑色,外部节点为黑色
- 红色节点不连续出现
- 在任意节点为根的子树中,所有外部节点的黑色深度相同,将其称为这棵树的黑色高度
递归定义
ARB 准红黑树:根节点为红色,其余特征满足红黑树
- 唯一一个外部节点(同时为根节点)构成黑色高度为0的红黑树RB~0~
- 对于h≥1,ARB~h~:根节点红色,左右子树均为RB~h-1~
- 对于h≥1,RB~h~:根节点黑色,左右子树分别为一棵RB~h-1~或ARB~h-1~
平衡性
对于T为RB~h~,有
- T有不少于2^h^-1个内部黑色节点
- T有不超过4^h^-1个内部节点
- 任何黑色节点的普通高度至多为其黑色高度的2倍
对于T为ARB~h~,有
- T有不少于2^h^-2个内部黑色节点
- T有不超过4^h^/2-1个内部节点
- 任何黑色节点的普通高度至多为其黑色高度的2倍
定理:假设T有n个内部节点,其普通高度不超过2log(n+1),查找代价始终为O(logn)
并查集
基本操作
并Union:将两个节点及其子树合并到同一类
查Find:查询这个节点的祖先根节点
并查集Uset用数组实现,内部为树结构
加权并
每次合并时,将节点数较少的树挂在节点数更多的树上,或者按秩,下面的代码为按数量
def Union(x, y):
x=find(x)
y=find(y)
if x == y:
return
if x.size()>=y.size():
uset[y]=x
x.size()+=y.size()
else:
uset[x]=y
y.size()+=x.size()
对于加权并,有k个节点的树其树高不超过$\left \lfloor logk \right \rfloor $(用数学归纳法证)
路径压缩查
将查询过程中遇到的节点均改为根节点的节点
def Find(x):#递归版
if x != uset[x]:
uset[x]=Find(uset[x])
return uset[x]
def Find(x):#非递归版
p=x
while uset[p]!=p:
p=uset[p]
while x != p:
uset[x],x = p,uset[x]
return p
性能
对于有n个元素的并查集,执行m次操作,其最坏情况时间复杂度为O((m+n)log*n)≈O(m+n)
| log*n是增长非常慢的函数,$log*(j)=\min{i\ | \ H(i)\ge j}$,其中H是以2为底的超指数函数 |
图遍历
DFS
算法
有向图
框架
颜色:白(未访问),灰(正在访问),黑:已结束访问
def DFS_Wrapper(Graph):
for v in Graph:
Initialize(v) #初始化节点v,缺省操作为将v颜色置为WHITE
for v in Graph:
if v.color == WHITE:
DFS(v)
def DFS(v):
ProcessNode(v) #预处理节点v,缺省操作为将v颜色置为GRAY
for w in v.neighbor:
if w.color == WHITE:
ProcessEdge(edge<v,w>) #预处理边vw
DFS(w)
BacktrackEdge(edge<v,w>) #处理遍历w所收集到的信息
else:
CheckEdge(edge<v,w>) #探测到已访问/正在访问节点的处理
PostorderProcessNode(v) #对v遍历完成后的处理,缺省操作为将v颜色置为BLACK
深度优先遍历树
TE:连接即将访问的“孩子”,即探寻到白色子节点
BE:连接“祖先”,即探寻到灰色节点
DE:连接非TE连接的后代,即探寻到黑色节点且有祖先/后继关系
CE:非上述情况,即探寻到黑色节点又无祖先/后继关系
活动区间
除缺省操作外,在处理函数中增加以下步骤
def Initialize(v): #初始化节点v,缺省操作为将v颜色置为WHITE
v.parent = None
def ProcessNode(v, time): #预处理节点v,缺省操作为将v颜色置为GRAY
time += 1
v.discoverTime = time
def ProcessEdge(edge<v,w>): #预处理边vw
w.parent = v
def PostorderProcessNode(v, time): #对v遍历完成后的处理,缺省操作为将v颜色置为BLACK
time += 1
v.finishTime = time
活动区间:active(v)=[v.discoverTime, v.finishTime]
活动区间的包含关系即反映了节点在深度优先遍历树中的祖先/后继关系
定理:
- w是v的后继节点$\iff$active(w)$\subseteq $active(v),当w不为v时为真包含
- w与v无祖先/后继关系$\iff$active(w)和active(v)互不包含
- 对于边vw,有如下等价关系:
- CE:active(w).finishTime < active(v).discoverTime
- DE:$\exist$ x,active(w)$\subset $active(x)$\subset $active(v)
- TE:$\nexists $ x,active(w)$\subset $active(x)$\subset $active(v)且active(w)$\subset $active(v)
- BE:active(v)$\subset $active(w)
- 白色路径定理:v是w的祖先$\iff$在发现v的时刻,存在v到w的白色路径
无向图
深度优先遍历树
与有向图相比,无向图:
- 不会有CE,因为如果y发现一个已访问且非祖先/后继关系x,那么访问到x时y是白色,应该会访问y
- BE:对于边vw,如果v是w的父节点,这种BE应剔除,因为在之前倍标记为了TE(二次遍历),故遇到灰色且非父节点则说明这条边是BE
- DE:如果发现边vw是DE,若w是白色,vw应该是TE,若灰色应该是BE,故只能是黑色,那么其在之前访问w时应该已经被标记为了BE(二次遍历)
- TE:与有向图类似,但是在无向图的深度优先遍历过程中为其做了定向
框架
颜色:白(未访问),灰(正在访问),黑:已结束访问
def DFS_UG(v, parent):
ProcessNode(v) #预处理节点v,缺省操作为将v颜色置为GRAY
for w in v.neighbor:
if w.color == WHITE:
ProcessEdge(edge<v,w>) #预处理边vw(TE)
DFS(w, v)
BacktrackEdge(edge<v,w>) #处理遍历w所收集到的信息
elif w.color == GRAY:
if w != parent:
CheckEdge(edge<v,w>) #探测到已访问/正在访问节点的处理(vw是BE)
#else:
# do nothing,是二次遍历
PostorderProcessNode(v) #对v遍历完成后的处理,缺省操作为将v颜色置为BLACK
应用
有向图
拓扑排序
可以拓扑排序$\iff$有向无环图DAG
DFS的顺序就应该是拓扑排序的排序,故可以增加如下操作:
def DFS_Wrapper(Graph): #初始化图,缺省操作为将节点置白色后循环对白色节点执行DFS
GlobalNum = Graph.size() + 1
def PostorderProcessNode(v, time): #对v遍历完成后的处理,缺省操作为将v颜色置为BLACK
GlobalNum -= 1
v.topoNum = GlobalNum
关键路径
任务调度:一组任务,之间的依附关系可以用有向图表示,节点为任务,权值为任务所需时间,边vw表示v依赖于w,即必须先完成w才能开始v。在任务调度问题中,我们认为有足够多的机器执行任务,故仅需要考虑任务间的依赖关系,关键路径即决定了所有任务完成所需的最短时间,它对任务优化有着指导意义:只有优化关键路径上的任务,才能减少整个时间
定义(最早开始时间est、最早结束时间eft):
- 一个任务$a_i$不依赖于任何任务,则$est_i$ = 0
- 一个任务$a_i$的$est_i$若已经被确定,则$eft_i$ = $est_i$+$l_i$
-
一个任务$a_i$如果依赖于其他任务,则$est_i =\max{eft_j\ \ a_i\to a_j}$
定义:(关键路径):任务调度中的关键路径是一组任务$v_0,v_1,…,v_k$满足:
- 任务$v_0$不依赖于任何任务(尽头)
- $\forall\ i \in [1,k],\ 有v_i\to v_{i-1},\ est_i = eft_{i-1}$
- $v_k$的最早结束时间是最大的
def CP_Wrapper(Graph):
for v in Graph:
v.color = WHITE, v.depend = None, v.est = 0
fin = -1
for v in Graph:
if v.color == WHITE:
DFS(v)
if fin < v.eft:
fin = v.eft
finpos = v
while finpos is not None:#这里用逆序输出
print finpos.name
finpos = finpos.depend
def CriticalPath(v):
v.color = GRAY
for w in v.neighnbor:
if w.color = WHITE:
CriticalPath(w)
if w.eft >= v.est:
v.est = w.eft
v.depend = w
v.eft = v.est + v.l
v.color = BLACK
强连通片
定义(强连通片、收缩图):如果有向图中任意两个节点相互可达,则为强连通图;将图G的每个强连通片收缩成点,强连通片之间的边(按照定义,边全是单向的)收缩为一条边,则为收缩图SCC
方法:
- 执行DFS,将尽头入栈
- 将图转置
- 依次出栈并作对于转置图的DFS,这次可达的点都为同一强连通片,因为按照栈的结构,每次拿出的节点若未被访问过,那么它就是在第一次DFS中,某次遍历的起始点,即转置图中的终点,它可达的点就均可达它
无向图
定义(k-点连通,k-边连通):任意去掉k-1个点/边,图仍然连通
当k=1时即为传统连通
因此,如果一个图不是2-点/边连通,必然存在至少一个点/边,去掉后就不再连通
定义(割点和桥):对于一个连通的无向图G,称点v为割点,如果去掉v后不再连通;称边uv为桥,如果去掉边uv后不再连通
寻找割点
v为割点$\iff$存在节点对w、x,v出现在w到x的所有路径上
基于DFS的割点定义:在一次DFS中,v不是根节点,则:v是割点$\iff$存在v的某棵子树,其中没有任何BE指向v的祖先节点
根据如上定义,维护discoverTime和back两个变量,discoverTime的定义和之前相同,为节点v发现时的时间,back作如下变化:
- 刚发现v时,v.back = v.discoverTime
- 遍历过程中遇到一条由v指向u的BE:v.back = min{v.back, u.discoverTime}
- 遍历v的子节点w结束,回退时:v.back = min(v.back, w.back)
可以看到,v.back只会越来越小,它标记的其实是它(及其所有子节点)可以连通到的最早的祖先的discoverTime,由于它指向父亲的那条边在第一次访问时被标记为TE,所以可以忽略。这样的话,如果遍历v的子节点结束,回退时发现:w.back≥v.discoverTime,就说明它的子树中没有任何BE指向祖先,根据定义,v是割点
def ArticulationPoint(v):
v.color = GRAY
time += 1
v.discoverTime = time
v.back = v.discoverTime
for w in v.neigbor:
if w.color = WHITE:
ArticulationPoint(w)
if w.back >= v.discoverTime:
ProcessAP(v) #v是割点
v.back = min(v.back, w.back)
else:
if edge<v,w> is BE: #w是灰色且非父
v.back = min(v.back, w.discoverTime)
v.color = BLACK
需要注意的是,按照定义,这个算法不适用于遍历树的根节点,其需要单独判断:若遍历结束时,root有至少2棵子遍历树,则root是割点,否则不是
寻找桥
基于DFS的桥定义:TE uv是桥$\iff$v为根的所有遍历树的子树中没有BE指向v的祖先节点(但可以指向v)
def Bridge(v):
v.color = GRAY
time += 1
v.discoverTime = time
v.back = v.discoverTime
for w in v.neigbor:
if w.color = WHITE:
Bridge(w)
if w.back > v.discoverTime: #w及其所有子树没有指向v及其祖先的
ProcessBridge(edge<v,w>) #vw是桥
v.back = min(v.back, w.back)
else:
if edge<v,w> is BE: #w是灰色且非父
v.back = min(v.back, w.discoverTime)
v.color = BLACK
BFS
算法框架
在广度优先中,虽然依然有三种颜色,但是对于一个节点我们会将其处理完再访问其他节点,之后不会返回该节点
广度优先中,灰色节点的意思更像是:在队列中,但还没有处理它
广度优先遍历中,需要维护一个队列
除了颜色,还可以为节点维护parent和dis信息,分别表示当前节点的父节点和当前节点到源节点的最短路径的长度,这些信息非常有用。利用parent回溯的路径就是源点到v的一条最短路径
def BFS_Wrapper(Graph):
for v in G:
v.dis = float("inf")
v.parent = None
v.color = WHITE
for v in G:
if v.color = WHITE:
BFS(v)
def BFS(v):
que = Queue.Queue()
v.color = GRAY
v.dis = 0
que.put(v)
while not que.empty():
w = que.get()
for x in w.neighbor:
if x.color = WHITE:
x.color = GRAY
x.parent = w
x.dis = w.dis + 1
que.put(x)
ProcessNode(w) #结束w的处理前做的操作
w.color = BLACK
广度优先中,队列具有如下性质:
若队列元素按顺序为$v_1, v_2,\ …\ ,v_k$,则有:
- $v_i.dis \le v_{i+1}.dis$
- $v_k.dis \le v_1.dis + 1$
第二点是由于广度优先是按“层级”的,只有相同的dis的节点访问完,才会访问dis+1的节点,dis+2的才有机会进入队列
广度优先遍历树
有向图
TE:遍历u时发现白色邻居v,则uv为TE
BE:遍历u时发现黑色邻居v,且v是u的祖先,则uv为BE,且有$v.dis< u.dis$
DE:不可能出现,因为一个节点会处理完
CE:遍历u时发现非白色邻居v,且v不是u的祖先,则uv是CE,且有$v.dis \le u.dis+1$
无向图
TE:类似有向图
BE:不存在,因为在那之前会被判断为TE
DE:不存在,类似有向图
CE:遍历u时发现灰色邻居v,则uv为CE,且$u.dis\le v.dis \le u.dis+1$
在无向图中,发现黑色节点就意味着是自己的父亲
应用
判断二分图
定义(二分图)将无向图G=<V,E>划分的顶点划分为$V_!,V_2$,若图中所有边均满足一个顶点在V1,一个顶点在V2,则称之为二分图,也就是说,划分内部没有边相连,或者说这个图是二着色的,即可以用两种颜色染色,使得每个点和其邻居颜色不同
算法过程为:在节点进队前,给当前节点染和父节点不同的颜色,在遇到非白色节点时判断颜色是否相同,相同则不是二分图,结束算法,直到结束也没遇到则是二分图
寻找k度子图
定义(k度子图)无向图G的子图H满足,每个顶点的度均不低于k
算法思路:先看所有节点,将度小于k的进队,如果度均大于k,则G本身就是k度子图,否则,按照BFS的顺序将这些节点出队,删除节点和它的边,并将与其相连的节点度-1、,若新节点度小于k则进队
算法结束后剩余的这些边和其顶点构成k度子图
图优化
最小生成树算法
n:点的个数;m:边的个数
对于稠密图,大致认为O(m)=O(n^2^),对于稀疏图,O(m)=O(n)
Prim算法
策略
贪心算法,每次选择和当前局部MST相连的边中权值最小的,然后更新
用优先队列存放
算法框架如下
def Prim(Graph):
pq=Queue.PriorityQueue()
MST=[]
for v in Graph:
v.state = UNSEEN
v.candidateEdge = None
v.weight = float("inf")
s=Graph[0] #随意挑选一个初始节点
s.state = SEEN
pq.put(-float("inf"),s)#将其权值设为0
while not pq.empty():
v = pq.get()
MST += v.candidateEdge #将边放入MST中
UpdateFringe(v, pq) #更新信息
def UpdateFringe(v, pq):
for w in v.nieghbor:
newWeight = edge<v,w>.weight
if w.state = UNSEEN:
w.state = SEEN
w.candidateEdge= edge<v,w>
w.weight = newWeight
pq.put(newWeight, w)
else:
if newWeight < w.weight: #发现了更小的边,需要更新
w.weight = newWeight
pq.decreaseKey(w,w.weight)
分析
正确性分析
最小生成树性质 给定图G的生成树T,T是最小生成树$\iff$T满足最小生成树性质,:对于任意不在T中的边e,$T\cup {e}$含有一个环,且e是环中权值最大的边
证明使用数学归纳法+反证(假设Prim算法某次选的边构造成T^k^,新加的边会成环(Prim算法下肯定选出来的是生成树),反证法证明这个边是环中权值最大的)
性能分析
分析算法过程,其代价为O(n*(进入队列+取出队列)+m*(更新队列))
基于堆的优先队列,其复杂度为O((m+n)logn)
Kruskal算法
策略
每次选权值最小的边,若这个边的两个端点未处于当前MST,则将这个边加入
使用并查集判断是否处于同一个MST
def Kruskal(Graph):
uset.init(Graph.V)
Edge = Graph.E
MST = []
sort(Edge)
for e in Edge:
if uset.Find(e.v) != uset.Find(e.u):
MST += e
uset.Union(e.v, e.u)
分析
正确性分析
设某一步选择了边e,e不在任何一个MST中,设有MST T,则$T \cup {e}$成环,证明:(1). 由于最小生成树性质,e是环上最大的边,(2). 由于Kruskal算法,环上有权值大于等于e的边(否则Kruskal不会选e)因此,有权值等于e的边,把它去掉、加入e,形成了新的MST
性能分析
O(边排序+m次Find和Union)
对于高效的并查集,和基于比较的排序,可以认为其效率为O(mlogm + n)或O(mlogm)或O(mlogn)
(O(logm) = O(logn))
MST的贪心构造框架MCE
切:将点划分两半
跨越切的边:边的两个顶点分别属于两半
MCE:跨越切的最小权值边
定理 对于某个边e,若存在某个切使其为MCE,则e属于某棵MST
MCE角度下的Prim算法:Prim算法每次选择一条MCE(切的一边是已有的点,另一边是剩下的点)
MCE角度下的Kruskal算法:每次选择一条MCE,将权值更小的避开,使其位于某个点集内部
最短路径
给定源点的最短路径
Dijkstra算法
每次选当前到源点的最短路的点,更新其邻居到源点的距离
正确性
需要每条边的权值都是非负的
性能分析
若使用堆作为优先队列,则为O((n+m)logn)
DAG的给定源点的最短路径
有向无环图→可以拓扑排序
def DAGG_SSSP(Graph, s): #s是给定的源点
for v in Graph:
v.dis = float("inf")
s.dis = 0
get topological order into L
for v in L:
if v is not s:
v.dis = min(u.dis+uv.weight for u in v.parent)
递归求解子问题
在拓扑排序中B和C都在其前面且指向D,由于其无环,D到S的最短路径就依赖于子问题B和C到S的最短路径
这一模板同样可以求最长路径等
所有点对间的最短路径
Floyd-Warshall算法
基于中继节点范围的递归
定义$I_i= {v_1, v_2, … ,v_i}$
定义子问题d(i, j, k)表示使用$I_k$的情况下,i到j的最短路径的长度,那么就有两种情况:①使用了k,则递归到子问题d(i, k, k-1)+d(k, j, k-1),②没使用k,递归到d(i, j, k-1)
def FloydWarshall(Graph):
#Graph是二维数组,存储节点间边的权值
D = Graph
for k in range(n):
for i in range(n):
for j in range(n):
D[i][j] = min(D[i][j], D[i][k] + D[k][j])
贪心
贪心遍历框架BestFS
每个节点分状态:
- Fresh 尚未涉及的节点
- Fringe 候选节点
- Finished 已完成的节点
框架如下:
def BestFirstSearch():
Initialize priorityqueue Fringe
Insert start node s to Fringe
while Fringe is not empty:
v = Fringe.ExtractMin() #取出优先级最高的候选节点并维护优先队列结构
ProcessNode(v)
UpdateFringe(v, Fringe)
def UodateFringe(v, Fringe):
for w in v.neighbor:
if w is Fresh:
Set the priority of w
Fringe.Insert(w, weight) #加入队列
elif w is Fringe:
update the priority of w
Fringe.DecreaceKey(w, newweight) #更新权值(如果需要的话)
代价为O(n*(ExtractMin + Insert) + m*DecreaceKey)
应用
相容任务调度
与之前的关键路径不同,这里的任务是互斥的,每个任务有开始时间和完成时间。问题的要求是找出最大的相容任务集
方法:选择“最早结束任务”的。将任务按完成时间先后排序,然后从前往后扫描,如果与已选择的冲突就忽略,否则就选择,其复杂度为O(nlogn)-每次挑选频率最低的合成一棵树,树的权值为频率之和,不断操作直到形成最终的2-tree,称之为Huffman tree,其复杂度为O(nlogn)
动态规划
dp的要素
- 重叠子问题 dp的核心问题是决定众多子问题计算的顺序(子问题间有相互依靠关系),从而消除重复计算
- 蛮力找最优 一般dp的解法是蛮力遍历找最优解,因此需要消除重复计算
- 最优子结构 大问题的最优解必然由小问题的最优解组合而成
应用举例
硬币兑换问题
- 输入:给定的n种面值的硬币$d_1, … , d_n$
- 输出:兑换N最少需要的硬币
贪心是不一定对的,例如有1元,4元,5元,要兑换8元
我们定义子问题coin[i, j]:用前i种硬币换j元,最少用多少硬币,其可以得到如下递归式:
$coin[i,j]=\left{\begin{matrix}{coin[i-1, j]} & 没有使用d_i\{coin[i, j-d_i]+1} & 使用了至少一个d_i \end{matrix}\right.$
在上述式子中,如果使用多个,则会在递归的子问题中处理
相容任务调度 dp
定义$S_{ij}$表示在任务$a_i$结束之后、$a_j$开始之前的任务的集合
定义$c[i,j]$表示子问题$S_{ij}$的解,即任务集合$S_{ij}$中最大相容任务的个数
假设选取了任务$a_k$,则后续只需要在任务集合$S_{ik}$和$S_{kj}$中选择即可,故有:
$c[i,j]=\left{\begin{matrix}{0} & S_{ij}为空\{\max_{a_k \in S_{ij}}(c[i,k]+c[k,j])+1} & S_{ij}不为空 \end{matrix}\right.$
计算复杂性理论初步
优化问题和判断问题
优化问题:输入结构,输出结构的优化指标的最值等
判定问题:输入结构和参数k,输出是否存在一个结构的指标和k满足某种关系
例如:
输入实例:无向图G
优化问题:求图G中最大团的大小
输入实例:无向图G,参数k
判断问题:是否存在大小为k的团
归约
P到Q的归约:P的输入x→Q的输入T(x),通过解决Q的算法判断yes/no
P对于输入x是yes$\iff$Q对于输入T(x)是yes
多项式时间归约
在归约中用的T的代价为输入规模的多项式,则称P可以多项式归约到Q,记为$P\le {_PQ}$
若$P\le {_PQ}$,$Q\le {_PR}$,则$P\le {_PR}$
P问题
多项式时间可解的问题,即存在关于n的多项式poly(n),存在解决P问题的一个算法,满足算法的代价$f(n)=O(poly(n))$
NP问题
多项式时间可验证的问题。
可验证指的是给出该问题的一个解,然后可以在多项式时间内验证其是否正确
NP难和NP完全
NP难
P是NP难,如果$\forall Q \in NP,Q\le {_PP}$
NP完全
NP且NP难
NP完全性的证明
证明Q是NP完全$\iff$ 证明一个NP完全问题$P\le {_PQ}$+证明Q是NP
其他补充
Hash表
设有n个元素,Hash表的大小为m
设负载因子$\alpha=\frac n m$
Closed Addr
即将冲突的放入一个链表中,也叫开散列
放入的方式为插入链表头部
性能分析
unsuc不成功搜索
不成功,即在这个位置的链表遍历完也没找到。定位到该位置代价为1。我们可以说,$\Theta(\alpha)$就是这个Hash表的链表的平均长度,故unsuc的代价为$\Theta(1+\alpha)$
suc成功搜索
假设$x_i$是第i个插入链表的元素
对于成功来说,是在总共有n个元素的情况下,某个元素成功的期望
找元素x成功的过程为:Hash到某位置(代价为1),在该位置的链表中找,并且找到了,故其代价为:$1+\frac 1n\sum_{i=1}^{n}(1+t)$
t为在链表中在x之前的元素个数
下面求t的期望
由于插入链表的头部,故t取决于在x之后插入的元素,故$t=\sum_{i+1}^{n}\frac1 m$
将其带入,进行计算,得到$1+\frac \alpha 2-\frac \alpha {2n}=\Theta(1+\alpha)$
Open Addr
即如果冲突且Hash表有空余,向后一直找,方法有线性探查法、二次探查法、双Hash(下次到哪由另一个Hash函数决定)等,又叫闭散列
性能分析
假设每一次冲突后向后查找的方法是一个大小为m的序列,即如果一直冲突,会按照某序列访问完所有格子
unsuc不成功搜索
失败,即一直冲突一直冲突,直到某次到一个空格子,则unsuc
在探测次数不少于i的情况下(即碰撞i-1次,第i次发现为空)
第一次冲突:$\frac n m$,第二次冲突$\frac {n-1} {m-1}$,…
$\frac n m\frac {n-1} {m-1}\frac {n-2} {m-2}……\frac {n-i+2} {m-i+2}\le{\frac n m}^{i-1}={\alpha^{i-1}}$
则平均情况下:
$\sum_{i=1}^{m}{\alpha^{i-1}}<\sum_{i=0}^{\infin}{\alpha^{i}}=\frac 1{1-\alpha}$
为什么是$\sum_{i=1}^{m}{\alpha^{i-1}}$?因为进行了i次的概率$\iff$进行了不少于i次的概率 - 进行了不少于i+1次的概率
suc成功插入
成功插入第i+1个插入链表的元素,即一个有i个元素、大小为m的表做了一次unsuc的搜索(然后找到一个空位),即$\frac 1 {1-\frac i m}=\frac m {m-i}$
故成功插入的代价为$\frac 1 n \sum_{i=1}^{n-1}{\frac m {m-i}}=\frac 1 \alpha \sum_{i=m-n+1}^{m}\frac1i\le \frac 1 \alpha\int_{m-n}^{m} \frac{dx}x=\frac 1 \alpha \ln{\frac1{1-\alpha}}$
平摊分析法
一些操作之间有关联性
聚类分析
在聚集分析中,要证明n个操作(可以是不同种类的操作)构成的操作序列在最坏情况下用时T (n),因此每个操作的平均成本为T(n)/n,例如:PUSH、POP、MULTIPOP。由于MULTIPOP内部是执行多个POP,而POP的执行次数最多和PUSH相当,故最坏情况用时O(n),三种操作的平摊代价为O(1)
记账法
“存款 & 取款”
有些操作的平摊代价大于实际代价,就把多余的部分当作存款,供那些实际代价大于平摊代价的操作使用
依然以上述为例,将PUSH的平摊低价分配为2,其余为0,即PUSH预支了POP的代价
势能法
与记账法等价,不同之处在于势能方法不是把账记在单个的对象上,而是记 全记在数据结构上
对一个初始数据结构$D_0$ 执行n个操作。对每个操作i,设 $c_i$ 为每个操作的实际代价,
$D_i $为对数据结构$D_{i-1}$执行第i个操作的结果. 势函数$\Phi$将每个数据结构$Di $映射为一个实数$Φ(D_i),$ 即与$D_i$相联系的势. 第i个操作的平摊代价 $a_i$ 根据势函数Φ 定义为
$a_i = c_i + Φ(D_i) - Φ(D_{i-1})$
每个操作的平摊代价为其实际代价 加上 由于该操作所增加的势。
n个操作的总的平摊代价为
$\sum a_i = \sum c_i +Φ(D_n) - Φ(D_0)$
如果我们能定义一个势函数Φ使得 对所有n,有$Φ(Dn) ≥ Φ(D_0)$,
则总的平摊代价∑ai就是总的实际代价∑ci的一个上界。通常为了方便起见定义Φ(D0) = 0。
直观上看,如果第i个操作的势差Φ(Di) - Φ(Di-1)是正的,则平摊代价ai表示对第i个操作多收了费,同时数据结构的势也随之增加了。如果势差是负值,则平摊代价就表示对第i个操作的不足收费,这是通过减少势来支付该操作的实际代价。
平摊代价依赖于所选择的势函数Φ。不同的势函数可能会产生不同的平摊代价,但它们都是实际代价的上界。最佳势函数的选择取决于所需的时间界。
依然以栈操作为例,定义势函数为栈中元素个数,对于PUSH来说,势差为+1,实际代价为1,故平摊代价为2;对于POP,势差-1,实际代价1,平摊代价0;MULTIPOP,势差-n,实际代价n,平摊代价0
对手论证
找下界的好方法
最坏情况下的最好下界:
用P表示问题,I表示问题的输入,A表示求解问题P的基于比较运算的算法,T(A,I)表示对于输入I算法A的计算时间复杂性
$U(n)=\min_{\forall A}{\max_{\forall I}{T(A,I)}}$
对手论证的基本思想:
对每一个A,构造一个输入特殊的输入I’,使T(A,I’)尽量地大,然后在所有A的集合上,求T(A,I’)的尽量好的下界作为f(n)。这种方法通过 $f(n) <= \min_{\forall A}{T(A,I’)}<= \min_{\forall A}{\max_{\forall I}{T(A,I)}}= U(n)$ 来保证f(n)是问题P的一个下界,又通过使T(A,I’)尽量大来保证f(n)是一个好的下界
对手论证的分析
- 算法设计者:尽量多的创造更多信息
- 算法分析者:尽量少的给予信息,拥有着随时合理改变取值的能力,从而做尽量多次的比较和判断
最后修改于2020-8-10
